Tuesday, August 31, 2010
Statistics and Market Research
It should be noted that not all commodities enjoy large sales even in communities that are thickly populated. Hence, a dealer in working clothes should take into account the number of farmers and laborers in the community, not the total population. Dealers in tractors, in farm machineries, and in agricultural implements may use agricultural income as a good index in determining their sales potentials. Dealers in gasoline should consider the number of motor vehicles in the place of business as a good measure of probable volume of sales.
kinds of set
The "I'm Pooped" Menu lol..
marapets word search answers
M7N1c - Integers
I usually don't venture into the 6-8 standards. But, since we discussed the compensation strategies recently, I thought I would discuss how two of those strategies can be used to derive the methods of calculations with integers.
Recall that the equal addition principle of subtraction states that if we add (or subtract) the same number to both the minuend and the subtrahend, the difference stays the same. Thus, 93 - 18 = (93 + 2) - (18 + 2) = 95 - 20. Another property of subtraction students encounter early on is that subtracting 0 will not change the number, that is A - 0 = A. By combining these two properties of subtracti! on, we can think about a problem like 8 - (-3) this way:
8 - (-3) = (8 + 3) - (-3 + 3) = (8 + 3) - 0 = 8 + 3."
Thus, you can see that subtracting a negative number is the same as adding the opposite.
We noted that there is a parallel between the compensation strategies for subtraction and division. We can actually use the equal multiplication principle of division to think about division of fraction problems, by combining it with another parallel property, dividing by 1 does not change the number. So, if you are given 3/5 ÷ 2/3, we can think like this:
Thus, we see that the division of fractions is the same as the multiplication by the reciprocal of the divisor.
Of course, strictly speaking, there is a minor glitch in both of these arguments. We established the four compensation strategies with whole numbers. But, we don't know if they still hold if we expand the range of numbers to integers/rational numbers. So, there is a circularity in these arguments. So, I'm not advocating these strategies to establish the computation algorithms, specially since there are other ways where students can meaningfully develop algorithms. However, I think these mathematical relationships are still interesting.
learn integers
Kinds of set
Example: Sets A, B, C, D are finite sets
2. Infinite set – uncountable
Example: Set E is an infinite set
3. Empty or null set – has no element
Example: A = { }
4. Equal set – set A and set B are equal set if the elements of set A is exactly the element of set B.
Example:
A = {set of an even counting number of one digit} = {2,4,6,8}
B = {set of an integral multiples of two having one digit = {2,4,6,8}
5. Equivalent set – two sets are equivalent if there exists a one-to-one correspondence between elements of the two sets.
Example:
A = {1, 2, 3, 4,5} - x coordinate
B = {6, 7, 8, 9, 10} – y coordinate
then &! #8220;A” is equivalent to B. We can construct the relation of set A and set B.
{ (1,6}, (2,7), (3,8), (4,4), (5,10) }
6. Subset – set whose elements are members of the given set A = {1,2,3,4,5,8}, B = {2,4,8}
7. Universal Set – totality of the given set with consideration. The set from which we select elements to form A given set is called universal.
Example:
Set A = {1, 2, 3, 4, 5, 8} is a universal set
Set B = {2, 4, 8} is a subset of set A
8. Disjoint Set – sets that has no common element ; if two sets have no element in common, the sets are called disjoint sets.
kinds of set
The Music Ensemble/Sports Team analogy
manager/coach=conductor/instructor (easy enough)
player (athlete)=player (musician) (as easy as it gets)
team practice=practicing instrument/music at home (I'll explain some of these more at the end)
regular season game=music ensemble rehearsal/class
playoff game=performance/concert
You may be asking: "W! hy isn't a rehearsal analogous to a practice and a performance analogous to a game?" Well, in most youth sports programs there are many games that lead up to some form of championship series. In most leagues, such a Little League, regular season games are all about equal playing time (as much as is possible) and learning the game. Team records in Little League are cleared at the beginning of the playoffs - all teams begin the post-season on equal footing. Only in the playoffs do wins and losses determine rank in the league.
In a music ensemble, there tend to be far fewer performances than games in a sports season. In fact, in most American educational ensembles (not just PMAC, but public schools and other music opportunities) there tends to be only one or two performanc! es at the end of a long series of rehearsals. The same weight ! is put o n such performances as is put on sports playoff games. Performances, like playoff games, are taken very seriously, even though the point (like in sports) is to experience the thrill and joy of participation in such an event. Good Little League programs are able to balance fun with the gravity of a playoff game, and good music programs are able to balance fun with the gravity of live performance in front of an audience.
Regular season games are very important. Each season I see my sons' teams improve vastly, especially in the area of defense (which is the aspect of baseball that requires the most team interaction), over the course of the regular season. It is the regular season games that provide the educational atmosphere that make compelling and well-played playoff games possible.
A baseball game can't be played without all 9 fielders, and some pitching and fielding relief in the dugout. Basically, a team plays at its best when everyone is present. The! same holds true for music ensembles. Whether an orchestra, rock band or sax quartet, all ensembles play their best when everyone is present. In a music ensemble, the need for all members to be present and playing is analogous to a team's need for all players at a regular season game.
In sports teams, practices are opportunities isolate fundamentals and work on drills. I see this as analogous to practicing one's part at home or in private lessons with a teacher. Just as a sports team can't run onto the field and play a game without practicing drills and learning rules in practice, a music ensemble can't play pieces of music in a rehearsal without the players practicing and learning their parts independently. Just as baseball players will practice fielding ground balls during drills at their team practice, music students should! be prac ticing isolated passages from their music in independent practice sessions and lessons. Yes, the first several rehearsals are spent putting isolated parts of music together, but in most music ensembles entire pieces are being played after the first couple rehearsals (if not from the very first rehearsal). And once the musical group starts playing full pieces in rehearsal, independent practice does not stop, but rather continues to be an important part of the preparation cycle.
As with all analogies, these comparisons are not iron-clad definitions. I present them purely to demonstrate expectation similarities. Similar to sports, each player in a music ensemble plays a specific, unique role. And as such, each player is as indispensable to their ensemble as a player is to his team.
In rehearsals, much like sports games, the absence of players creates challenges that are sometimes impossible! to overcome. When there aren't enough players to field, games are forfeited, and teams miss the opportunity to prepare for the playoffs. When playing in an ensemble, the same level of commitment is expected of a musician as is expected of an athlete on a sports team. And when student musicians rise to the occasion, remarkable things happen. That is why a spectacular music performance can often give audiences the same feelings of excitement and joy that sports fans experience during a playoff win.
is to as is to analogy
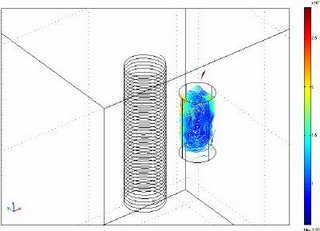
A COMSOL Multiphysics Application : Induction Stirred Ladle
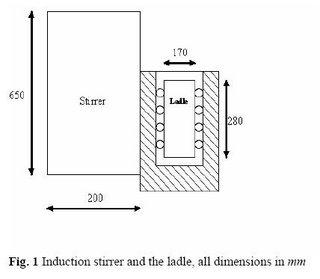
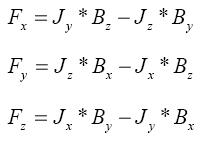 These force field are fed into the NS or K-e model as source term for obtaining the solution of the velocity field in the melt. The Modelling is then done as follows:
These force field are fed into the NS or K-e model as source term for obtaining the solution of the velocity field in the melt. The Modelling is then done as follows:
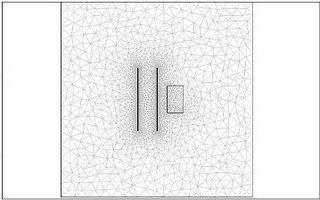
The Results are shown here in 2D and 3D
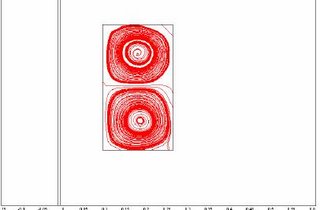
initial value problem calculator
Vedic Mathematics Lesson 43: Polynomial Division 1
You can find all my previous posts about Vedic Mathematics below:
Introduction to Vedic Mathematics
A Spectacular Illustration of Vedic Mathematics
10's Complements
Multiplication Part 1
Multiplication Part 2
Multiplication Part 3
Multiplication Part 4
Multiplication Part 5
Multiplication Special Case 1
Multiplication Special Case 2
Multipli! cation S pecial Case 3
Vertically And Crosswise I
Vertically And Crosswise II
Squaring, Cubing, Etc.
Subtraction
Division By The Nikhilam Method I
Division By The Nikhilam Method II
Division By The Nikhilam Method III
Division By The Paravartya Method
Digital Roots
Straight Division I
Straight Division II
Vinculums
Divisibility Rules
Simple Osculation
Multiplex Osculation
Solving Equations 1
Solving Equations 2
Solving Equations 3
Solving Equations 4
Mergers 1
Mergers 2
Mergers 3
Multiple Mergers
Complex Mergers
Simultaneous Equations 1
Simultaneous Equations 2
Quadratic Equations 1
Quadratic Equations 2
Quadratic Equations 3
Quadratic Equations 4
Cubic Equations
Quartic Equations
In the previous lesson, we identified one of the solutions to a quartic equation based on the values of the coefficients of the different powers of the unknown variable, x. Once the solution is identified, we needed to perform a polynomial division to get the residual cubic equation from the given quartic equation and one of its solutions. We touched upon the procedure for performing this tangentially, but we did not take it up formally. In this lesson, we will formalize the procedure for performing simple polynomial divisions. In particular, we will deal with the div! ision of higher-order polynomials by polynomials of the first degree (linear polynomials) in this lesson. In future lessons, we will deal with divisions where the divisor is a polynomial of higher degree.
In the most general terms, in this lesson, we are dealing with divisions of the following form:
Divide ax^n + bx^(n-1) + ... + constant by (cx + d)
In the previous lesson, (cx + d) was either (x + 1) or (x - 1). But the method we used in that lesson is applicable to other divisors also. We already know how to do some basic divisions without even realizing we are doing polynomial division. As in any other division, the answer will have a quotient and a remainder. In some cases, the remainder may be zero. In some cases, the quotient may be zero too.
Consider the following example of division by a linear polynomial, wh! ich practically anyone can actually perform without any hesita! tion:
Divide 4x^2 + 6x + 7 by 2x.
In this case, c = 2 and d = 0. Just by inspection, we can say that the quotient of this division is 2x + 3, and the remainder is 7. The way to verify whether we obtained the correct answer, just as in the case of arithmetic division is to check whether dividend = quotient * divisor + remainder.
In the above case, we can indeed verify that 4x^2 + 6x + 7 = 2x*(2x + 3) + 7. Thus, we can be confident that our division was correct.
Now, consider another example of polynomial division which may not be readily apparent as polynomial division. Divide 4x^2 + 6x + 7 by 2. In this case c = 0 and d = 2. Once again, just be inspection, we can say that the quotient is 2x^2 + 3x + 3, and the remainder is 1. We can verify that this is the correct answer by seeing that 4x^2 + 6x + 7 = 2*(2x^2 + 3x + 3) + 1.
However, when neither c nor d is zero, the situation becomes trickier. That is the kind of divisio! n that is not dealt with in school in any detail. It is the kind of division that is not taught to students as a normal part of algebra education for whatever reason. It is actually very useful to teach this kind of division, as we will see later in this lesson!
Consider the division of 4x^2 + 6x + 7 by x + 2. Essentially, we have to find (4x^2 + 6x + 7)/(x + 2). How exactly do we perform this division? The answer turns out to be quite simple actually. We have already seen some examples of how we do such a division in the previous lesson. Let us formalize the method in this lesson.
Consider the division of a polynomial ax^n + bx^(n-1) + ... + constant by the first degree expression cx + d. Consider the ratio c/d. The secret to polynomial division is to rewrite the numerator using this ratio just like we did in our lessons on cubic equations and quartic equations.
We have to rewrite the dividend in the form below:
ax^n + e! x^(n-1) + fx^(n-1) + ... + yx + zx + constant1 + constant2
And the coefficients have to satisfy the conditions below:
c/d = a/e = f/g = ... = z/constant1
e + f = b
...
y + z = coefficient of x in the given dividend
constant1 + constant2 = constant
In some cases, constant2 could be zero. When that is the case, the division does not have a remainder. When constant2 is not zero, that is the remainder (at least an intermediate remainder) of the division.
Let us see how these rules are applied in the case of (4x^2 + 6x + 7)/(x + 2). In this case, c/d = 1/2. Thus, we have to rewrite the dividend using the ration 1/2.
4x^2 + 6x + 7 = 4x^2 + ax + bx + constant1 + constant2
where
1/2 = 4/a = b/constant1
a + b = 6
constant1 + constant2 = 7
We see that we can accomplish this by writing the dividend as below:
4x^2 + 8x - 2x - 4 + 11
This can then be factorized as below:
4x(x + 2) - 2(x + 2) + 11
Consider (4x^3 + 6x^2 - 8x + 15)/(2x - 1). In this case, c/d = -2/1. Thus, we rewrite the dividend using this ratio as below:
4x^3 -2x^2 + 8x^2 - 4x - 4x + 2 + 13
We can then factorize the expression above as below:
2x^2(2x - 1) + 4x(2x - 1) - 2(2x - 1) + 13
Thus, the quotient of the division is 2x^2 + 4x - 2, and the remainder is 13.
Now, consider (3x^4 + 4x^3 - 11x^2 + 6x - 5)/(2x + 1). In this case c/d = 2/1. Thus, we rewrite the dividend using this ratio as below:
3x^4 + 1.5x^3 + 2.5x^3 + ! 1.25x^2 - 12.25x^2 - 6.125x + 12.125x + 6.0625 - 11.0625
!
We can then factorize the expression as below:
1.5x^3(2x + 1) + 1.25x^2(2x + 1) - 6.125x(2x + 1) + 6.0625(2x + 1) - 11.0625
The quotient is then (1.5x^3 + 1.25x^2 - 6.125x + 6.0625), and the remainder is -11.0625. We can rewrite the quotient as 24x^3/16 + 20x^2/16 - 98x/16 + 97/16, and the remainder as -177/16. Thus, the quotient can be rewritten as (24x^3 + 20x^2 - 98x + 97)/16, and the remainder is -177/16.
Thus, we see that the quotient and remainder can contain fractional terms. And, in this case, the remainder was negative too! Thus, polynomial division can result in some results that can cause us to scratch our heads. But, we can verify that the answer we got is correct by simply multiplying the quotient with the divisor, and adding the remainder to the result to see whether we get back our original dividend.
Now consider a division as below:
(2x^3 + 5x^2 - 6x + 8)/(2x + 2)
We see that the ratio c/d ! in this case is 2/2 = 1. Thus, we could rewrite the dividend expression as below:
2x^3 + 2x^2 + 3x^2 + 3x - 9x - 9 + 17
We would then factorize it as below:
2x^2(x + 1) + 3x(x + 1) - 9(x + 1) + 17
We immediately see that the expressions in the parentheses are x + 1, not our divisor, 2x + 2. Thus, if we decide, based on the factorization, that our quotient is 2x^2 + 3x - 9, with a remainder of 17, we will find that we are wrong. In fact, (2x^2 + 3x - 9)(2x + 2) + 17 = 4x^3 + 10x^2 - 12x - 1, which is not what we started with as our original dividend. This, then tells us that the actual factorization of the rewritten dividend is as below:
x^2(2x + 2) + (3x/2)(2x + 2) - (9/2)(2x + 2) + 17
Thus, the quotient would be (x^2 + 3x/2 - 9/2) and the remainder would be 17. This can be verified as the correct answer. Thus, we need to pay extra attention when the ratio c/d can be simplified by the presence of common! factors. The common factor, in this case, prevented us from ! getting the divisor as a common factor during the factorization when we factorized the rewritten dividend. We then had to introduce fractions during the factorization to get the divisor as the common factor during the factorization.
A simpler solution to the above problem would be to take the common factor out of the divisor and divide the dividend by this common factor in advance. In this case, the common factor in the divisor is 2. So, we can convert the dividend to x^3 + (5/2)x^2 - 3x + 4 before we attempt the division. Now, our division problem is reduced to (x^3 + (5/2)x^2 - 3x + 4)/(x + 1). The ratio of terms in the divisor is 1/1 = 1. Thus, we can perform the division by rewriting the dividend as below:
x^3 + x^2 + (3/2)x^2 + (3/2)x - (9/2)x - 9/2 + 17/2
This will then enable us to perform the factorization as below:
x^2(x + 1) + (3x/2)(x + 1) - (9/2)(x + 1) + 17/2
The quotient is then x^2 + 3x/2 + 9/2. But since w! e divided the numerator and denominator by the common factor, 2, remember that the remainder is now to be multiplied by this common factor to get the final remainder. Thus, the remainder is not 17/2, but is instead 17!
Having fractional terms as part of the dividend may appear a little intimidating. So, another solution would be to take the common factor out of the divisor and keep it aside. Perform the division as usual, then divide the resulting quotient by the common factor.
In this case, our initial division resulted in a quotient of 2x^2 + 3x - 9. We see that we can then divide this by the common factor, 2, to get the correct quotient. Remember not to divide the remainder by the common factor!
Now, let us consider the last special case. Consider the division of 6x + 7 by x + 1. In this case, the dividend is also a linear polynomial. But the method is still the same as before. The ratio, c/d, in this case is 1/1 = 1. Thus, we r! ewrite the dividend expression as below in preparation for fac! torizati on:
6x + 6 + 1
This then leads to the factorization as below:
6(x + 1) + 1
We then conclude that the quotient is 6 and the remainder is 1.
Let us now record our observations about polynomial division, with a first-degree polynomial as the divisor, below:
- The quotient will be a polynomial of one degree lower than the original dividend (thus, if the dividend is also a linear expression, as in our last example, then the quotient will be just a constant with no x term)
- The remainder will be a constant, but can be either positive or negative
- If the divisor has a constant as a common factor, we can set the constant aside, divide by the divisor reduced to lowest terms, then divide the quotient by the common factor to get the correct quotient (no change needs to be made to the remainder)
- Alternatively, we can divide the dividend by the common factor, then perform the division by the div! isor reduced to lowest terms to get the quotient, then multiply the remainder by the common factor to get the correct remainder
As you can see, the division of a polynomial by a linear polynomial is quite easy once the method of ratios is laid out. This is an application of the Madhyamadhyena Adhyamanthyena sutra. Now, as promised, let us examine why this technique is useful. The secret to its usefulness lies in the insight that practically every real number is a polynomial. Consider the number 324, for instance.
324 = 3*10^2 + 2*10 + 4
This is the same as 3x^2 + 2x + 4, where x = 10! In fact, we can even express it is 3x^2 + 3x - 6, where x = 10. In fact there are several ways to express a given number as a polynomial, even using just x = 10. Using a different value of x enables us to rewrite the number in other bases (such as octal, where x = 8, hexadecimal, where x = 16 and binary, where x = 2). Because of this, it is easy to ! see that we can use our insights from polynomial division to p! erform r egular arithmetic division with just as much ease! In fact, this is the practical application of polynomial division that I have been hinting at since the beginning of this lesson!!
Take the case of 324/11 for instance. This can be rewritten as (3x^2 + 2x + 4)/(x + 1), where x = 10. We already know how to do this with no problems. We rewrite the dividend expression as below:
3x^2 + 3x - x - 1 + 5
We then factorize it to get:
3x(x + 1) -1(x + 1) + 5
We then conclude that the quotient is 3x - 1 and the remainder is 5. 3x - 1 when x = 10 is 29. Thus, we have just performed the division, 324/11 and found that the quotient is 29 with a remainder of 5. I encourage you to verify that this is indeed correct! Let us now take on a few more examples to see just how easy the method is.
Take 372/12 for instance. This can be rewritten as (3x^2 + 7x + 2)/(x + 2) where x = 10. The ratio, c/d, is then 1/2. We can th! en rewrite the dividend expression as below, and factorize it:
3x^2 + 6x + x + 2, which can be factorized as
3x(x + 2) + 1(x + 2)
Thus, we see that the quotient is 3x + 1 (or 31 with 10 as the value of x), and the remainder is 0!
Now, let us take a few slightly trickier cases. Consider 412/12, for instance. This can be rewritten as (4x^2 + x + 2)/(x + 2), where x = 10. The ratio, c/d is once again 1/2. Then, the dividend can be rewritten and factorized as below:
4x^2 + 8x - 7x - 14 + 16 which can be factorized as
4x(x + 2) - 7(x + 2) + 16
This then tells us that the quotient is 4x - 7 (or 33, since x = 10), and the remainder is 16. This can not be correct. We can verify using a calculator that the quotient in this case should be 34 and the remainder should be 4. It turns out that our solution is correct, but it does not meet the standards for normal division. In particular, in this case, the remainder ! turned out to be bigger than the divisor. To correct this, ad! d one to the quotient and reduce the remainder by the divisor. If necessary, repeat the operation until the remainder becomes less than the divisor. Following this procedure, we can then adjust our solution to a quotient of 34 (add one to 33), and a remainder of 4 (subtract the divisor, 12, from the original remainder of 16). Now, we can say that the answer is in truly correct form!
Now consider the case of 271/13. This can be rewritten as (2x^2 + 7x + 1)/(x + 3), where x = 10. The ratio, c/d is 1/3 in this case. We can then rewrite the dividend expression, and do the factorization as below:
2x^2 + 6x + x + 3 - 2 which can be factorized as
2x(x + 3) + 1(x + 3) - 2
We can then interpret this as saying that the quotient is (2x + 1), or 21 since x = 10, and the remainder is -2. Once again, we are left with an answer that seems wrong. We are not used to dealing with negative remainders when we do divisions normally. But the correction for t! his problem, once again, is very simple. We simply subtract one from the quotient and add the divisor to the remainder. Repeat this until the remainder is positive. Thus, we can correct our answer to a quotient of 20 (subtract 1 from 21), and a remainder of 11 (add the divisor, 13, to -2). It is easy to verify that a quotient of 20 and a remainder of 11 is indeed correct.
Next, let us consider 4878/18. We can write it as (4x^3 + 8x^2 + 7x + 8)/(x + 8), where x = 10. But the ratio, c/d now becomes 1/8. Using that ratio, we would be forced to rewrite the dividend expression as below:
4x^3 + 32x^2 - 24x^2 - 192x + 199x + 1592 - 1584
Obviously, this is correct, and does give us the following factorization:
4x^2(x + 8) - 24x(x + 8) + 199(x + 8) - 1584
This then translates to a quotient of 4x^2 - 24x + 199, which equals 400 - 240 + 199 = 359, and a remainder of -1584. To get this answer to standard form would require ! a lot of subtractions of 1 from the quotient and additions of ! 18 to th e remainder!
Instead, let us consider a different approach to this problem. We can rewrite the given problems as (4x^3 + 8x^2 + 7x + 8)/(2x - 2), where x = 10. Now, we see that c/d = -1 and the divisor has a common factor of 2. Let us take the common factor out initially and do the rewriting and factorization as below:
4x^3 - 4x^2 + 12x^2 - 12x + 19x - 19 + 27 which can be factorized as
4x^2(x - 1) + 12x(x - 1) + 19(x - 1) + 27
This translates to a quotient of 4x^2 + 12x + 19, which can be translated as 539 by substituting x = 10. Now, remember to divide the quotient by 2 (the common factor in the divisor), and we get 269.50. Since the remainder is greater than 18, we also have to subtract 18 from it and add 1 to the quotient. This gives us a quotient of 270.50 and a remainder of 9. Since 0.50*18 is 9, we can further simplify it to a quotient of 270 with a remainder of 18 (subtract the 0.50 from the quotient and add 0.50*18 to the! remainder), which once again can be reduced to a quotient of 271 with no remainder. We can verify that this is indeed the correct answer.
The approach we took the second time around is reminiscent of the use of vinculums in various arithmetic operations. Vinculums are dealt with in great detail in a lesson dedicated to them. It may be useful to review that lesson once more for more insights into the usefulness of the concept of vinculums.
Now, let us consider a more tricky case. We will try 3421/77. This can be rewritten as (3x^3 + 4x^2 + 2x + 1)/(7x + 7), where x = 10. We see that there is a common factor of 7 in the divisor, and a c/d ratio of 1. Using the ratio, we can rewrite the dividend and factorize it as below:
3x^3 + 3x^2 + x^2 + x + x + 1, which can be factorized as
3x^2(x + 1) + x(x + 1) + 1(x + 1)
This directly translates to a quotient of 311 with a remaind! er of 0. We now have to remember to divide the quotient by the common factor, 7. This presents us problems since we are left with another division problem almost as difficult as the original problem. However, we have reduced the problem by at least an order of magnitude, and in fact, we can perform the division by 7 in our heads to get a final quotient of 44 and a remainder of 3. Notice that this remainder is from a division by 7 while the real remainder needs to be from a division by 77. So, to get the true remainder to the problem, we now multiply this remainder of 3 from this step by 77/7 (original divisor/common factor), which is 11. Thus, the final answer is 44 with a remainder of 33.
An easier way to remember this might be to express the answer as 44 and 3/7 with a remainder of 0. Now, we convert the 3/7 to the final remainder by multiplying by the divisor, 77, to get 33 as the final remainder. We can verify that 44*77 + 33 = 8843, so we know our answer is c! orrect.
To obviate the need for a manual division, we can once again the use the concept of vinculums to rewrite the given problem as (3x^3 + 4x^2 + 2x + 1)/(8x - 3). This then gives us a c/d ratio of -8/3. But this leads to new problems as we see below:
3x^3 + 4x^2 + 2x + 1 can be rewritten with a ratio of -8/3 as
3x^3 - (9/8) x^2 + (41/8)x^2 - (123/64)x + (251/64)x - 753/512 + 1264/512 which can be factorized as
(3/8)x^2(8x - 3) + (64/41)x(8x - 3) + (512/251)(8x - 3) + 1264/512
This then gives us a quotient of 300/8 + 640/41 + 512/251 (after substituting x = 10 in the expression above) with a remainder of 1264/512. As you can see, this is not a very convenient expression to work with and convert into a standard form for presentation as a normal quotient and remainder. So, the lesson to take away from this is to be careful and not carried away by vinculums too much!
The concept of polynomial division is useful to le! arn since it can translate directly into an easy method for ar! ithmetic division also. But, sometimes, it does not produce results any faster or easier than other methods of division. This is important to recognize as a shortcoming of the method. Different methods have their own strengths and weaknesses. If the ratio we need to work with is inconvenient and can not be converted into a more convenient ratio by the use of vinculums or other tricks, we have to recognize that polynomial division may not be the best approach to the division problem.
Moreover, in this lesson, we have dealt with only linear divisors. This can limit the technique to just 2-digit divisors under most conditions. We will leave this lesson with an example of a division by a 3-digit divisor, but in general, we will deal with division by more digits in the next lesson, when we will deal with polynomial division where the divisor is not linear.
Consider the division problem 8843/126. This can be expressed as (8x^3 + 8x^2 + 4x + 3)/(x^2 + 2x + 6), ! where x = 10, but this does not leave us with a linear divisor. Instead, let us rewrite this as (8x^3 + 8x^2 + 4x + 3)/(12x + 6), where x = 10. Now, we have a linear divisor, so we can proceed as before. We see that the ratio c/d = 2, and 6 is a common factor in the divisor. We will set aside the common factor for now, and rewrite and factorize the dividend as below:
8x^3 + 4x^2 + 4x^2 + 2x + 2x + 1 + 2 which can be factorized as
4x^2(2x + 1) + 2x(2x + 1) + 1(2x + 1) + 2
This then translates to a quotient of 421, and a remainder of 2. Since we took out a common factor of 6 from the divisor, we now divide the quotient by 6. Dividing 421 by 6 gives us the new quotient of 70 and a remainder of 1. To convert this remainder to a remainder that would be obtained by division by 126 rather than by 6, we need to multiply it by 126/6, which is 21. Now, we add this remainder to the remainder from the factorization to get a final remainder of 23.
An easier way to remember this might be to express the ! result o f the division as 70 and 1/6. To move the 1/6 to the remainder, we need to multiply it by the divisor, 126. This gives us 21, which is then added to the already existing remainder of 2 to give us a final remainder of 23. We can verify that 70*126 + 23 = 8443, so we know that our answer is correct.
As you can see, polynomial division has several uses, chief among them, the factorization of polynomial expressions. But, as we saw in this lesson, it can also translate into an easier way to do some arithmetic divisions also. Hope you will take the time to practice some of the techniques, both with polynomial expressions as well as with arithmetic expressions, so that you can be confident about their application when it is appropriate. Good luck, and happy computing!
how to do polynomials
Get Help or Give Help at Free Student Tutoring, Adult Literacy, Special Needs Programs Starting at TLE
When he was in middle school, my son was stymied by math courses taught in classrooms packed by 25-30 kids and only one teacher. It wasn't until he began to work with a tutor that some of the mysteries of math began to reveal themselves - enough that he could pass the classes.
It's a given in the world of education that the best way to learn something is through one-on-one tutoring. But because of the lack of resources, very few students - from grade-school-age through adult - are fortunate enough to get that kind of tutoring. For every student like my son who was lucky to get tutoring, there are thousands more who need it but don't have access to it.
That's one big reason why the TLE Educational Network is launching a free tutoring program at its virtual education center in Second Life!
The tutoring program is one of three new educational initiatives TLE has designed and is announcing during this week's Grand Opening events (see list at end of this post), and is extending a warm invitation to anyone interested in tutoring or mentoring to join in.
Students Improve through Tutoring
This virtual education tutoring program will use two! methods to provide assistance:
- One-on-One Tutoring: TLE will link those wanting assistance in a particular area of study with a tutor who can help them. Language arts, sciences, and math are the major focuses, but other subjects may be available, too. Any student and any tutor from anywhere in the world can sign up to give or receive tutoring through the TLE Educational Network in SL, and the student and tutor will work together at times and in ways convenient for them.
- Study Hall: TLE is setting up blocks of time when tutors are available at TLE in Second Life, and anyone can come to get remedial assistance. Students can bring their homework, assignments, and questions and work with a tutor in a group setting. The mentors will not do the work for the students, but will help them to better understand the subject.
Learning Challenge! s Support
People with dyslexia, autism, and other special needs often face major obstacles in getting educational assistance. The Internet, and particularly a virtual world like TLE inhabits, is a perfect learning and support environment for people dealing with special needs and those who support/help them.
Through its Learning Challenges Support group, TLE will offer special tutoring, mentoring, and sharing/support programs that will help those with learning challenges master their studies - and will also establish a network for sharing ideas, support, and group programs for people who have special needs and for those who are their support system.
Adult Literacy
The third educational service TLE is launching in Second Life will be an in-depth program to help adults who want to lear! n to read English, or to read it better. With both t! he U.S. adult illiteracy rate and illiteracy rates around the world being so high, there's a strong need for more help - especially assistance that is free to the receiver.
"At TLE we know if you are Illiterate you live in a very scary world and TLE would love to help you in any way possible." ~ TLE Board Sponsor of the Adult Literary program
The Adult Literacy Program will start at the bare minimum with skills such as letter recognition, phonics, and work towards reading at a first-grade level. After some time, students will move on to more advanced reading.
Tutors in the Adult Literary program will also help people with job applications, legal for! ms, etc.
How to Participate in These Programs
1) Those who wish to participate as students or tutors in any of these programs are encouraged to join any or all of the new TLE groups for these programs.
There are several ways to join the groups (which are not Second Life groups, so they do not take up an SL group slots):
- In Second Life, go to the tutoring corner of the TLE Educational Network Student Lounge, where you'll find signs for the three groups, as well as additional information. Click the sign(s) for the groups you wish to join.
- Or go to the TLE Groups Room, which displays signs for all of its special-interest groups, as well as the general group. Click the sign(s) to join the group(s).
- Or access the TLE Groups Web page, where you can type in your SL avatar name and select the groups you wish to join.
(You can learn more about how TLE's groups function and how you receive information from them by checking out this post.)
2) Let us know how you'd like to participate - as either a learner or a tutor.
- Go to the TLE Student Lounge tutoring corner (shown in above photo).
- Click the purple sign to receive a notecard.
- Fill in the notecard.
- Drop it into the black mailbox in that same corner of the lounge.
3) TLE will follow up with you based on what you've indicated.
Tutoring/mentoring programs such as these are incredibly rewarding for everyone involved - and can make a huge difference in the lives of the individuals, their communities, and the entire world. I look forward to hearing the success stories that I know will come from these virtual education support programs at TLE.
Grand Opening Week at TLE Educational Network January 13-17, 2010Special Events Each Day: | |
| Wednesday, Jan. 13 12:30 p.m. SLT | WAR MEMORIAL DEDICATION at TLE War Memorial Complex: Dedication of Memorial Fountain with comments by fountain designer Aelwyn Fields Comments by Holocaust survivor Fela "Fanny" Starr Bagpipe music by The PipeDreams Group |
| Thursd! ay, Jan. 14, two times: 12-2 p.m. AND 6-8 p.m. SLT | JOB FAIR at TLE Publishing House Building Information about teaching & other positions available at TLE |
| Friday, Jan. 15: 12 noon to 2 p.m. SLT 2-4 p.m. SLT | STUDENTS' DAY at TLE Creative Arts Building Games Tournament '50s Sock Hop Dance with dance music provided by DJ Peris Ashton |
| Saturday, Jan. 15 11 a.m. to 12:30 p.m. SLT | GARDEN PARTY DANCE & AMERICAN CANCER SOCIETY FUNDRAISER at TLE Getrost Magic Gardens Welcome by Eagle Himmel, TLE teacher Dancing for fun & fundraising Live music by Idella Quandry (Alicia Morgan), keyboard player/singer/songwriter |
| Sunday, Jan. 17 11 a.m. to 12:30 p.m. SLT | GALA GRAND OPENING BALL at TLE Publishing House Building Introduction of Adult Literacy and Special Challenges Groups Ballroom dancing Music provided by O! nlyHalfCrazy Gumbo |
free tutors
DON'T FEEL GUILTY: EAT DESSERT!
equivalent resistance calculator
Congratulations Matt!

Matthew Babbitt (at left above, celebrating after NYSML with teammates Zubin Mukerjee, Gili Rusak, Cecilia Holodak, and Jien Ogawa) scored high enough on the notoriously challenging 2010 USA Math Olympiad contest to qualify for an invitation to this summer's Math Olympiad Summer Program.
Congratulations! You are among a very small group of about 57 students (from the original pool of over 221,000 AMC 10 and AMC 12 participants) invited to take part in! the 2010 Mathematical Olympiad Summer Program (MOSP) scheduled to begin Tuesday, June 8 and ending Wednesday, June 30, 2010. This year’s MOSP will be held on the campus of the University of Nebraska-Lincoln.
The purpose of the program is to broaden the participants’ view of mathematics and foster their excitement toward further study. It will better prepare you for possible future participation on our International Mathematical Olympiad team as well as for possible careers involving mathematics.
Full days of classes, problem solving and tests give students extensive preparation in several important areas of mathematics, including algebra, geometry, combinatorics, number theory, and many other special topics. All members of the MOSP staff are housed with the students, and will closely interact with all the participants outside of class as well. In the past this interaction has greatly contributed to the development of Ame! rica’s most talented young mathematicians.
Ple ase note that basic MOSP expenses for food and lodging will be covered by the MAA American Mathematics Competitions. We will also reimburse your round-trip travel expenses up to $400 (see attached MOSP Acceptance and Travel Agreement). Additional information about MOSP can be found in the Student Handbook. You will also receive a set of MOSP Medical Forms that your parent/guardian will need to complete, and return to us so they arrive by May 26, 2010.
I am pleased to invite you to the 2010 MOSP, and feel that this program will offer you three weeks of camaraderie with many of our country’s top math students, and activities which will make a significant difference in your mathematical education.
Sincerely,
Prof. Steven R. Dunbar
AMC Director
Cc Zuming Feng, MOSP Academic Director
Some of the factors that have contributed to Matthew's success:
1) M! atthew delights in working with other students in our high school math circle and has been a key leader in our middle school math circles as well. He exemplifies one of the mottos of our math circle: the more of your mathematical understanding you share with others, the more you have for yourself. Answering the questions of other students who are struggling with a problem you believe you have solved deepens your understanding of that problem. The relationship between mentors/mentee or collaborators is mutually beneficial: the whole really is more than the sum of the parts. The photo at the top of this post shows Matt celebrating at NYSML with some of our math circle students who have enjoyed working with Matt over the past two years, starting out in our middle school math circle, where Matt has been a leader, and have now moved up to our high school math circle: Zubin Mukerjee, Gili Rusak, Cecilia Holodak, and Jien Ogawa. His interactions with them and with many ot! her math circle members, seasoned veterans and fresh-faced roo! kies ali ke, have advanced his understanding of mathematics. In a very real sense, all members of our math circle can claim a share of the credit for his success.
2) Matthew likes to write about mathematics! He has sharpened his mathematical expository skills in many ways.
An informal, free, and fun way to start out writing about math is to participate in the Art of Problem Solving forums, where Matthew has been an active participant. Choose an interesting problem posted by another participant who wants to discuss solutions and post your ideas about how to solve it. Or post a question of your own that you've been struggling with and would like to discuss in order to understand it better. Putting your question in writing can help you sharpen your understanding of the problem. Writing down a clear description of your attempt at solving a problem forces you to think explicitly about some of t! he assumptions you are making.
Once a student develops comfort in writing in that informal, friendly, and highly interactive environment, the way paved for the student to move to writing in more formal settings, such as mathematics journals that post challenging problems and welcome well-written student submissions.
The Canadian Mathematical Society publishes an excellent journal called Crux Mathematicorum with Mathematical Mayhem. They post challenging problems in each issue in their "Mathematical Mayhem" section. The currently open problems are here. (They are published in French and English, so if your French is sketchy, just scroll down the PDF to the English version.) Anyone who would like to try to solve these problems is welcome to mail in their solution to Crux before June 15. The na! mes of all successful submitters will be published in an issue! next fa ll. In addition, Crux publishes an examplary solution to each problem in that subsequent issue as well.
Browsing through recent issues of Crux, you can see that Matthew has submitted a number of correct solutions to problems this past year, and they even published one of his solutions as a highlighted solution as well. Check out problem M379 on pages 429-430 to see Matthew's published solution to a problem submitted by Professor McLaughlin of the University of New Brunswick. It's fun and fascinating to see the diversity of the names, affiliation, and hometowns of the other people who submitted correct solutions to the same problem. In this case, the other successful submitters are listed by Crux as: Edin Ajanovic, First Bosniak High School, Sarajevo, Bosnia and Herzegovina; George Apostolopoulos, Messlonghi, Greece; Antonio Godoy Toharia, Madrid, Spai! n; Richard I. Hess, Rancho Palos Verdes, CA; R. Laumen, Derne, Belgium; Richard Peiró, IES "Abastos", Valencia, Spain; Mridul Singh, student, Kendriya Vidyalaya School, Shillong, India; Neculai Stanciu, George Emil Palade Secondary School, Buzău, Romania; Edward T.H. Wang, Wilfrid Laurier University, Waterloo, ON, and Jixuan Wang, student, Don Mills Collegiate Institute, Toronto, ON. (It's interesting to note that Jixuan was a member of the Canadian team at the 2009 International Physics Olympiad, where he won a silver medal, and it looks like he is leading contender for this year's team as well. Sharpening those expository writing skills comes in handy in physics too! Jixuan has also done very well on the Canadian Math Olympiad.)
There are other journals that publish excellent problems and welcome student submissions, including the Mathematical Association of America's Math Horizons magazine, where Albany Area Math Circle student Felix Sun submitted a solution that was published as a highlighted solution last year. Other magazines where you can look for problems include: the American Mathematical Monthly, Mathematics Magazine, the College Mathematics Journal, the Harvard College Math Review, and the Pi Mu Epsilon Journal.
Stop by a library at a local college and you can easily browse through recent issues of most of these journals. The Harvard College Math Review appears to have gone into a latent stage, but you can find interesting back issues to browse here.
It should be noted that all these journals welcome submissions of original problems. Most of the problems they publish are submitted by their readers. Composing a good pro! blem can be a great way to develop your problem solving abilities. Matthew has also had one of his problems published in Crux. (Check out Problem M410 of the November issue to see Matt's problem. The list of successful solvers and a highlighted solution submitted by a reader will no doubt appear in an upcoming issue. It will be fun to see the names and hometowns of those who have worked on Matt's problem. Maybe someday he will meet one of the solvers at the International Math Olympiad!
Problems on Area of a circle
Statistics calculators
These are the different types of calculators available:
ANALYSIS OF VARIANCE (ANOVA)
BETA FUNCTION
- Beta Function Calculator
- Incomplete Beta Function Calculator
- Regularized Incomplete Beta Function Calculator
CONFIDENCE INTERVALS
- Confidence Interval Calculator (R-Square)
- Confidence Interval Calculator (Regression Coefficient)
- Confidence Interval Calculator (Regression Intercept)
- Correlation Coefficient Calculator (from Covariance)
- Significance of Correlation Coefficient Calculator
CUMULATIVE DISTRIBUTION FUNCTION (CDF)
- CDF Calculator - Fisher F Distribution
- CDF Calculator - Noncentral F Distribution
- CDF Calculator - Normal Distribution
- CDF Calculator - Standard Normal Distribution
- CDF Calculator - Student's t-Distribution
- Effect Size Calculator (Hierarchical Multiple Regression)
- Effect Size Calculator (Multiple Regression)
- Effect Size Calculator (Student's t-Test)
FISHER F-DISTRIBUTION
- Critical-F Calculator
- Cumulative Distribution Function Calculator (Fisher F Distribution)
- Fisher F Calculator (Hierarchical Multiple Regression)
- Fisher F Calculator (Multiple Regression)
- Cumulative Distribution Function Calculator (Noncentral F-distribution)
- p-Value Calculator (Fisher F-test)
- Probability Density Function Calculator (Fisher F Distribution)
- Gamma Function Calculator
- Incomplete Gamma Function Calculator
- Incomplete Gamma Function Calculator (Complemented)
- Incomplete Gamma Function Calculator (Lower Limit of Integration)
- Incomplete Gamma Function Calculator (Upper Limit of Integration)
- Area Under the Standard Normal Curve Calculator (Cumulative)
- Area Under the Standard Normal Curve Calculator (One-Tailed)
- Area Under the Standard Normal Curve Calculator (Two-Tailed)
- Cumulative Distribution Function (CDF) Calculator for the Normal Distribution
- Cumulative Distribution Function (CDF) Calculator for the Standard Normal Distribution
- Probability Density Function (PDF) Calculator for the Normal Distribution
- Probability Density Function (PDF) Calculator for the Standard Normal Distribution
- Standard Normal Curve Z-Score Calculator
- A-priori Sample Size Calculator (Hierarchical Multiple Regression)
- Beta (Type II Error Rate) Calculator (Hierarchical Multiple Regression)
- Effect Size Calculator (Hierarchical Multiple Regression)
- Fisher F Calculator (Hierarchical Multiple Regression)
- Post-hoc Statistical Power Calculator (Hierarchical Multiple Regression)
MISCELLANEOUS
- Adjusted R2 Calculator (Population R-Square)
- Fisher's Exact Test Calculator (2 x 2 Contingency Table)
- Z-Score Calculator (Standard Score)
- A-priori Sample Size Calculator (Multiple Regression)
- Adjusted R2 Calculator (Population R-Square)
- Beta (Type II Error Rate) Calculator (Multiple Regression)
- Confidence Interval Calculator (R-Square)
- Confidence Interval Calculator (Regression Coefficient)
- Confidence Interval Calculator (Regression Intercept)
- Effect Size Calculator (Multiple Regression)
- Fisher F Calculator (Multiple Regression)
- Post-hoc Statistical Power Calculator (Multiple Regression)
- p-Value Calculator (Chi-Square test)
- p-Value Calculator (Correlation Coefficient)
- p-Value Calculator (Fisher F-test)
- p-Value Calculator (Fisher's Exact Test)
- p-Value Calculator (Normal Curve - Cumulative)
- p-Value Calculator (Normal Curve - One-Tailed)
- p-Value Calculator (Normal Curve - Two-Tailed)
- p-Value Calculator (Significance of Mediation)
- p-Value Calculator (Student's t-Test)
- PDF Calculator - Fisher F-Distribution
- PDF Calculator - Normal Distribution
- PDF Calculator - Standard Normal Distribution
- PDF Calculator - Student's t-Distribution
- A-priori Sample Size Calculator (Hierarchical Multiple Regression)
- A-priori Sample Size Calculator (Multiple Regression)
- A-priori Sample Size Calculator (Student's t-Test)
- Post-hoc Statistical Power Calculator (Hierarchical Multiple Regression)
- Post-hoc Statistical Power Calculator (Multiple Regression)
- Post-hoc Statistical Power Calculator (Student's t-Test)
- A-priori Sample Size Calculator (Student's t-Test)
- Beta (Type II Error Rate) Calculator (Student's t-Test)
- Cumulative Distribution Function Calculator (Student's t-Distribution)
- Effect Size Calculator (Student's t-Test)
- p-Value Calculator (Student's t-Test)
- Post-hoc Statistical Power Calculator (Student's t-Test)
- Probability Density Function Calculator (Student's t-Distribution)
- Student's t Calculator
The website link is: Statistics calculators
Posted by: Tim Sandle
Z score probability calculator
Prime Number Program : Java Programming
import java.io.*;
class PrimeNumber {
public static void main(String[] args) throws Exception{
int i;
BufferedReader bf = new BufferedReader(
new InputStreamReader(System.in));
System.out.println("Enter number to Check:");
int num = ! Integer. parseInt(bf.readLine());
System.out.println("Prime number: ");
for (i=1; i < num; i++ ){
int j;
for (j=2; j<i; j++){
int n = i%j;
if (n==0){
break;
}
}
! if(i == j){
System.out.print(" "+i);
}
}
}
}
What is a prime number